Data Task

The data task calculates the positions for the motors to make the drawing. When first run, the data task reads in an .hpgl file selected by the value of the shared variable image (set in the Interface Task), then sets the calculated variable to False, triggering the next section. This section parses the .hpgl file and uses the Newton-Raphson function (described below) to calculate the necessary motion of the motors.

TaskDataFunctions.NewtonRaphson(fnc, jacobian, guess, thresh, targ)

Determines the roots (or zeros) of a function by iteratively solving the equation while varying the inputs until the result equals zero. More specifically, each each iteration is solved using

\[x_{n+1} = x_n - \frac{f(x_n)}{\frac{\partial f}{\partial x}}\]

This approaches the x-intercept of the function with every iteration.

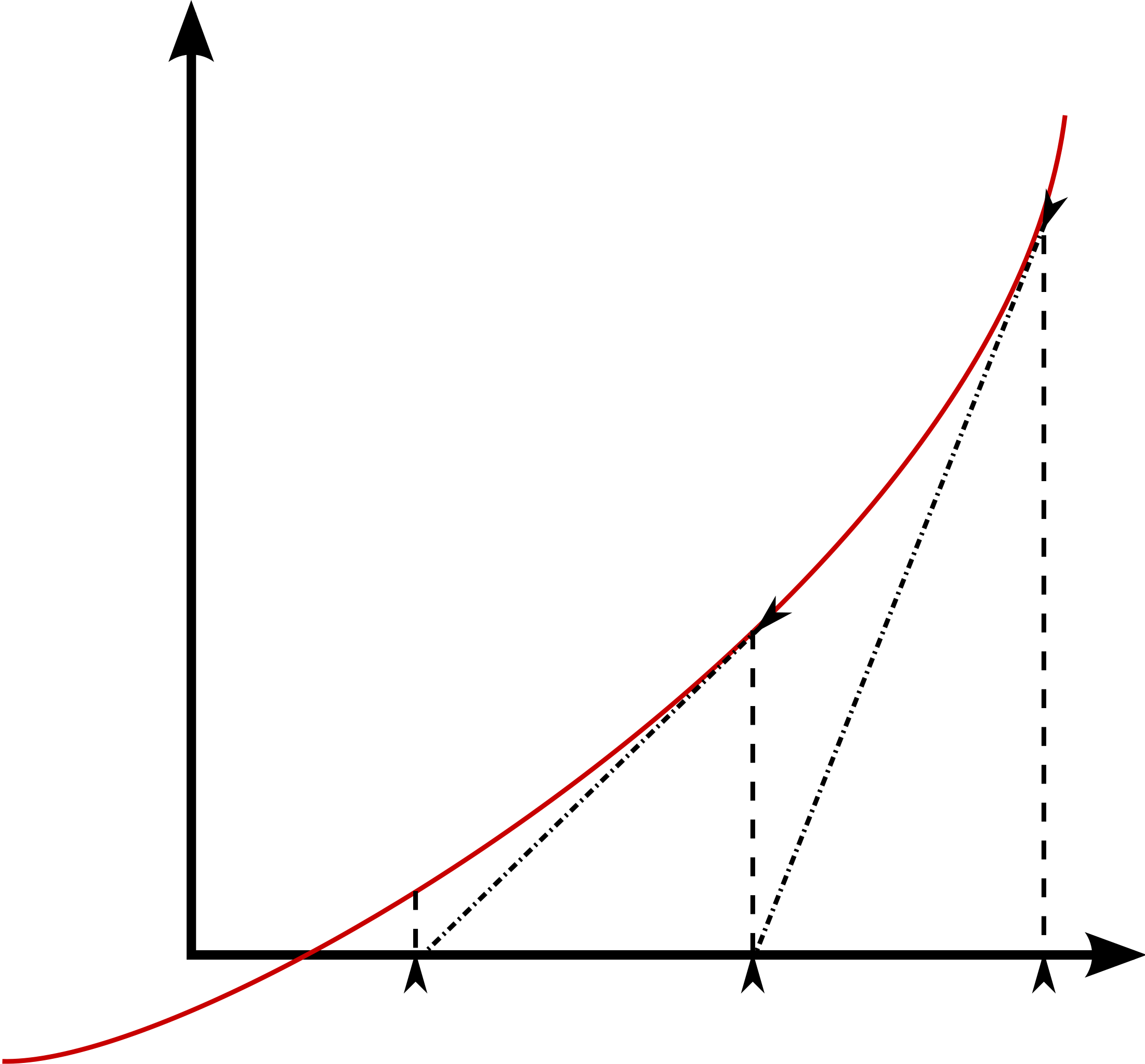
It is important to note that this method relies on a somewhat accurate initial initial guess, otherwise the algorithm could converge on the wrong zero point.

TaskDataFunctions.dg_dtheta(theta)

Partial derivative of position with respect to theta. This is the negative of the jacobian, and is passed into the Newton-Raphson function. It is calculated from the motor positions (in radians) using the following equations

\[ \begin{align}\begin{aligned}\frac{\partial g}{\partial \bar{\theta}} = \begin{bmatrix} f_{0,0} & f_{0,1}\\\ f_{1,0} & f_{1,1}\\\end{bmatrix}\end{aligned}\end{align} \]

where

\[ \begin{align}\begin{aligned}f_{0,0} &= \frac{k \theta_1}{l} \\\ f_{0,1} &= \frac{-k \theta_2}{l} \\\ f_{1,0} &= \frac{k \theta_1 \left( \frac{k (\theta_{1}^2 - \theta_2^2)}{2 l} - \frac{l}{2} \right)}{l\sqrt{k\theta_2^2- \left( \frac{k (\theta_1^2 - \theta_2^2)}{2 l} - \frac{l}{2} \right)^2}} \\\ f_{1,1} &= -\frac{2k\theta_2 + \frac{k\theta_2}{l^2} \left(k(\theta_1^2-\theta_2^2)-l^2 \right)}{2\sqrt{k\theta_2^2- \left(\frac{k(\theta_1^2 - \theta_2^2)-l^2}{2l}\right)^2}}\end{aligned}\end{align} \]

In these equations, \(l\) refers to the distance between the pivots (10 in) and \(k\) is the coefficient which converts motor angle to linear position of the arm. The derivation of \(k\) can be found under Analysis section on the Mechanical Design page.

Parameters

theta – The set of the two motor angles (in radians)

TaskDataFunctions.draw(i)

Runs the Newton-Raphson function for each of the X Y points in the desired drawing.

Parameters

i – Iterator to move through the list of X Y points.

Return theta_calc

The resulting motor angles from the Newton-Raphson function.

TaskDataFunctions.g(pos, theta)

This function represents the forward kinematics for the system. It accepts a target position in X Y coordinates, as well as positions of the two motors, and returns an error value: the difference between them.

\[err = \bar{X}_{targ} - \bar{f}(\theta)\]

where

\[ \begin{align}\begin{aligned}f_x(\theta_1, \theta_2) &= \frac{k \left(\theta_{2}^2 - \theta_{1}^2\right)}{2 l} + \frac{l}{2}\\ f_y(\theta_1, \theta_2) &= \sqrt{k \theta_{2}^2 - \left(\frac{k \left(\theta_{2}^2 - \theta_{1}^2\right)}{2 l} + \frac{l}{2}\right)^2}\end{aligned}\end{align} \]

where \(k\) refers to the conversion factor between motor angle and power screw position, and \(l\) refers to the distance between the two pivot points; 10 inches in our case. K is derived on the Mechanical Design page under Analysis.

Parameters

• pos – Target position in X Y coordinates

• theta – A set of theta values describing the position of the motors.

TaskDataFunctions.move(draw, vals)

Groups a set of X Y points into a ‘shape,’ returning a set of points and a True/False value representing pen-up or pen-down.

Parameters

• draw (boolean) – Indicates if the pen should be up or down for this shape.

• vals (string) – The .hpgl row that contains the points for the shape.

Returns

A list of the form [Pen up/down value, X values, Y values].

Return type

list